Introduction:
This unit, our class learned about constant acceleration, and created the Constant Velocity Particle Model.
Instantaneous Velocity:
1. The first way of finding the instantaneous velocity is to determine the slope of the tangent to an x vs. t graph at a given point.
2. The second way is to use the mathematical model:
vf=at+vi
(Final Velocity = acceleration * time + Initial Velocity)
Two graphs depicting velocity vs. time and position vs. time
Displacement:
1. The first way of finding the displacement of an object is to find the area under a V vs. T curve. This process is demonstrated in the V vs T graph above.
2. The second way is to use the mathematical model:
x = 1/2at^2 + vit
(positon = 1/2 acceleration * time squared + initial velocity * time)
Acceleration:
1. The first way of finding the acceleration of an object is to find the slope of a v vs. t graph
2. Using the mathematical model:
a = change in v / change in t
3. Solving for acceleration in the mathematical model:
x = 1/2at^2 + vit
(positon = 1/2 acceleration * time squared + initial velocity * time)
4. Solving for acceleration in the mathematical model:
vf=at+vi
(Final Velocity = acceleration * time + Initial Velocity)
x vs. t graphs:
1. With a position vs. time graph, you can find the starting position, direction of motion, and velocity. You can also use the graph to draw a v vs. t graph or an a vs. t graph.
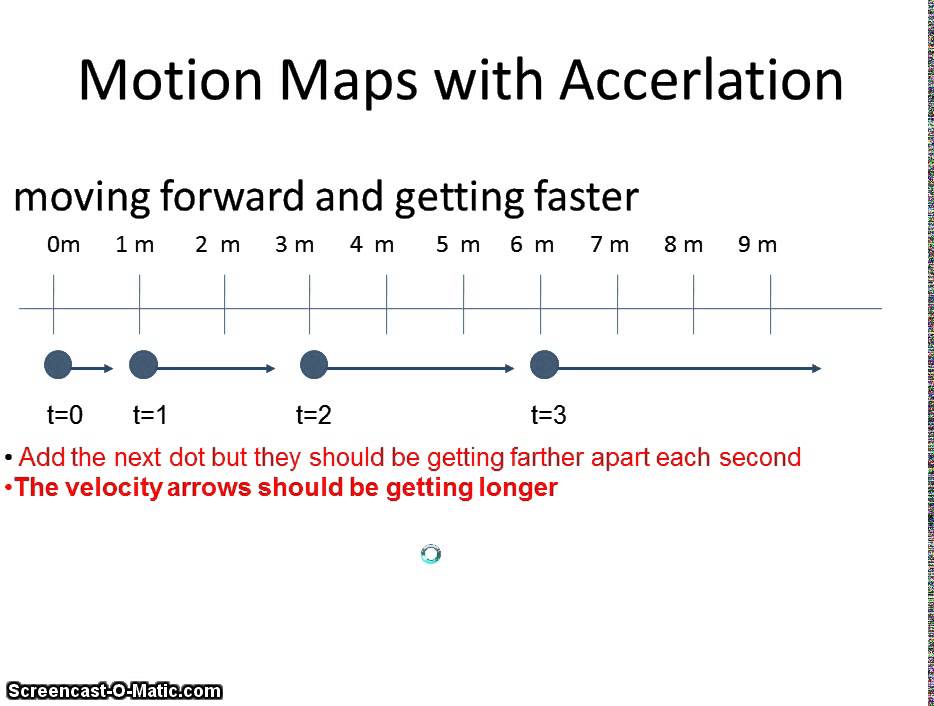
2. You can use the information to draw a motion map
3. You can determine the average and instantaneous velocity (as mentioned above).
4. You can determine the displacement (as mentioned above)
 |
| The x vs. t graphs are showing constant acceleration |
1. With a velocity vs. time graph, you can find the acceleration (explained above), and find the direction of motion (positive or negative slope).
2. You can use it to draw an x vs. t graph
3. You can use it to draw an a vs. t graph
4. You can use it to draw a motion map (with velocity and acceleration vectors
 |
| Motion map showing constant acceleration |
No comments:
Post a Comment